The mechanical properties of materials are the performance exhibited by materials when subjected to external forces.
Elasticity#
The ability of a material to not undergo permanent deformation under the action of external forces.
Elastic limit#
$ \sigma_e=\frac{F_e}{A_0} $
Where $ F_e $ is the elastic limit load, measured in N, and $ A_0 $ is the original cross-sectional area of the specimen, measured in $ mm^2 $.
Stiffness#
The ability of a material to resist elastic deformation under the action of external forces.
According to Hooke's law:
$ \sigma = E\varepsilon $
Where $ E $ is the elastic modulus, measured in MPa, which represents stiffness.
Strength#
The ability of a material to resist deformation and failure under the action of external forces.
Yield strength#
The ability of a material to resist plastic deformation.
$ \sigma_s=\frac{F_s}{A_0} $
Where $ F_s $ is the load at yield of the specimen, measured in N.
0.2% offset yield strength#
For plastic materials that do not exhibit significant plastic deformation, the stress value at which a 0.2% permanent deformation is produced is called the 0.2% offset yield strength.
$ \sigma_{0.2}=\frac{F_{0.2}}{A_0} $
Where $ F_{0.2} $ is the load at which a 0.2% residual plastic deformation is produced, measured in N.
Tensile strength#
The ability of a material to resist being pulled apart under tension, and is the maximum stress the material can withstand before fracture.
$ \sigma_b=\frac{F_b}{A_0} $
Where $ F_b $ is the maximum load before fracture of the specimen, measured in N.
Hardness#
The ability of a material to resist localized deformation, specifically the ability to resist penetration by other hard objects.
Generally, materials with higher strength also have higher hardness.
Brinell hardness (HB)#
A specific load $ F $ is applied to the surface of the material being tested using a hardened steel ball or hard alloy ball with a diameter of $ D $. After a certain period of time, the load is removed and the hardness value is determined based on the indentation area.
This method is usually used to test softer materials such as annealed, normalized, and tempered steel, cast iron, and non-ferrous metals.

Vickers hardness (HV)#
A diamond indenter with an angle of $ 136^\circ $ is used to create a square pyramid-shaped indentation on the material surface under a load $ F $ (in kgf). The diagonal length $ d $ (in mm) of the indentation is measured, and the indentation area $ A $ (in $ mm^2 $) is calculated. The hardness value is expressed as $ F/A $.
This method is especially suitable for testing the hardness of very thin layers, such as metal coatings, thin metal sheets, carburized or nitrided parts.

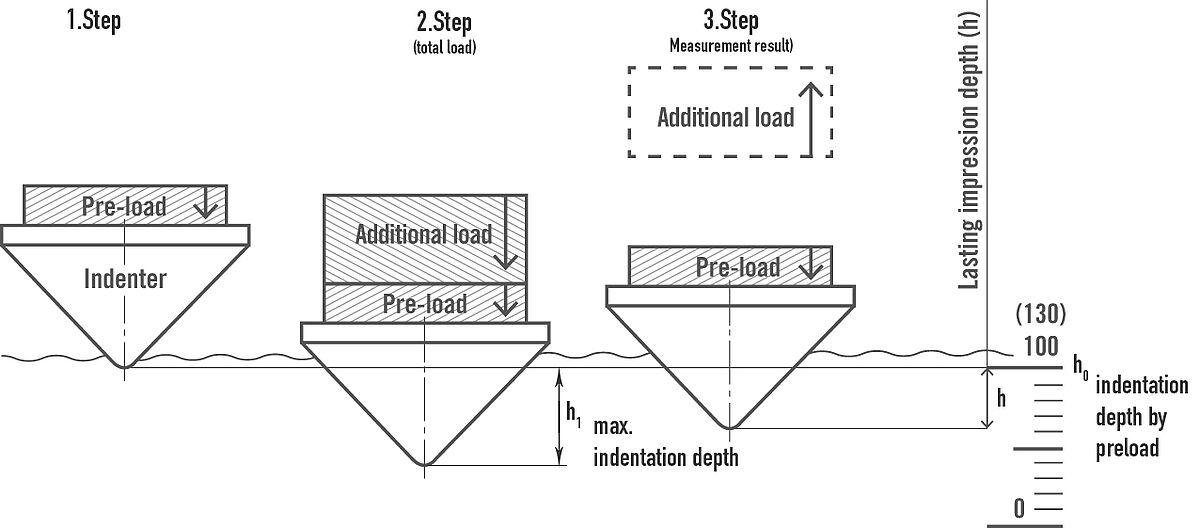
Rockwell hardness (HR)#
A diamond or steel standard indenter with a cone angle of $ 120^\circ $ is used to apply a specified load to the surface of the material being tested. The hardness value is determined based on the depth of the indentation.
This method is commonly used to test harder materials such as hardened steel and tempered steel.
Plasticity#
The ability of a material to undergo permanent deformation under stress without fracturing.
Reduction of area#
$ \psi = \frac{A_0-A_1}{A_0}\times 100% $
Where A1 and A0 are the cross-sectional areas at the fracture point and the original cross-sectional area of the specimen, measured in $ mm^2 $.
Elongation#
$ \delta = \frac{L_0-L_1}{L_0}\times 100% $
Where L1 and L0 are the lengths at fracture and the original gauge length of the specimen, measured in mm.
Toughness#
A measure of the energy required for a material to fracture.
Impact toughness#
The ability of a material to resist failure under impact loads. The impact work $ A_k $, measured in J, is the energy consumed when the specimen fractures:
$ A_k = mg\cdot h_1 - mg\cdot h_2$
The impact toughness value $ a_k $ is the impact work per unit cross-sectional area at the notch, used to indicate the size of the material's impact toughness, measured in J/cm^2:
$ a_k = \frac{A_k}{A_0} $
Generally, materials with good plasticity also have higher toughness.
The relationship between strength, hardness, plasticity, and toughness of materials:
Generally, materials with higher strength have higher hardness.
Generally, materials with better plasticity have higher toughness.
Generally, as the strength and hardness of a material increase, its plasticity and toughness decrease.
Fatigue strength#
Fatigue#
The phenomenon of fracture occurring in a material under alternating loads below its yield strength.
Fatigue strength#
The maximum stress a material can withstand under a specified number of alternating loads without fracturing, represented by $ \sigma^{-1} $, commonly known as the fatigue limit.
For steel materials, $ \sigma^{-1} $ is approximately half of its yield strength $ \sigma_b $, while for non-metallic materials, $ \sigma^{-1} $ is usually much lower than that of metals.
Specified number of cycles:
Steel materials: $ 10^7 $
Non-ferrous metals and their alloys: $ 10^8 $
This article is also synchronized to xLog by Mix Space.
The original link is https://nishikori.tech/posts/tech/Mechanical-properties-of-materials