材料の力学的性能は、材料が外力に対して示す性能です。
弾性#
材料は外力の作用下で永久変形を生じない能力を持ちます。
弾性限界#
$ \sigma_e=\frac{F_e}{A_0} $
ここで、$ F_e $ は弾性限界荷重であり、単位は $ N $ です。$ A_0 $ は試験片の元の断面積であり、単位は $ mm^2 $ です。
剛性#
材料は外力の作用に対して弾性変形に抵抗する能力を持ちます。
フックの法則によると:
$ \sigma = E\varepsilon $
ここで、$ E $ は弾性率であり、単位は $ MPa $ で剛性を表します。
強度#
材料は外力の作用に対して変形と破壊に抵抗する能力を持ちます。
降伏強度#
材料は塑性変形に抵抗する能力を持ちます。
$ \sigma_s=\frac{F_s}{A_0} $
ここで、$ F_s $ は試験片の降伏時の荷重であり、単位は $ N $ です。
条件降伏強度#
明らかな塑性変形がない塑性材料は、$ 0.2% $ の永久変形が発生した時の応力値を降伏強度とし、条件降伏強度と呼ばれます。
$ \sigma_{0.2}=\frac{F__{0.2}}{A_0} $
ここで、$ f_{0.2} $ は試験片が $ 0.2% $ の残留塑性変形を生じた時の荷重であり、単位は $ N $ です。
引張強度#
材料は引張力の作用に対して引き裂かれる能力を持ち、材料が破断する前に耐えられる最大応力です。
$ \sigma_b=\frac{F_b}{A_0} $
ここで、$ F_b $ は試験片が破断する前の最大荷重であり、単位は $ N $ です。
硬度#
材料は局所的な形状変化に抵抗する能力を持ち、他の硬い物体が表面に侵入するのを防ぎます。
通常、材料の強度が高いほど、硬度も高くなります。
ブリネル硬度 HB(Brinell-hardness)#
特定の荷重 $ F $ を使用し、直径 $ D $ の焼入れ鋼球または硬質合金球を被験材料の表面に押し込み、一定の時間後に荷重を取り除き、圧痕の面積に基づいて硬度値を決定します。
通常、退火、正火、焼入れ鋼、鋳鉄、非鉄金属などの比較的柔らかい材料のテストに適しています。

ヴィッカース硬度 HV(Vickers-Hardness)#
頂角が $ 136^\circ $ のダイヤモンドピラミッドを使用し、荷重 F($ kgf $)の作用下で、材料表面に四角錐状の圧痕が生じ、圧痕の対角線の長さ $ d $($ mm $)を測定し、圧痕の面積 $ A $($ mm^2 $)を計算し、$ F/A $ の値で硬度値を表します。
特に金属めっき、薄板金、カーボン化または窒化された部品の表面硬度など、非常に薄い層の硬度を測定するのに適しています。

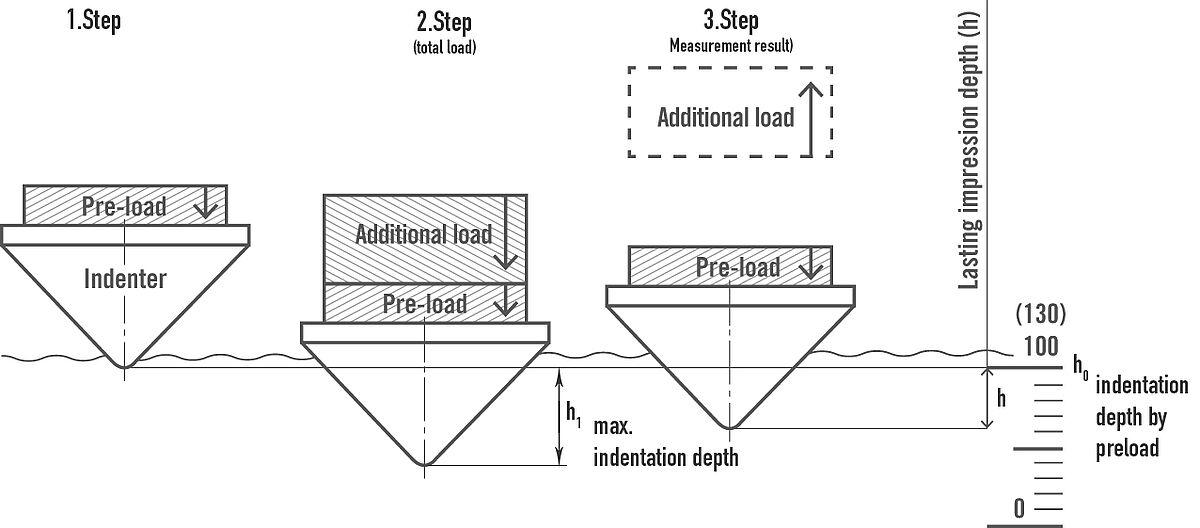
ロックウェル硬度 HR(Rockwell-Hardness)#
$ 120^\circ $ の錐度を持つダイヤモンドまたは鋼製の標準インデンタを使用し、規定の圧力で被験材料の表面に押し込み、圧痕の深さに基づいて硬度値を決定します。
焼入れ鋼、調質鋼などの比較的硬い材料のテストによく使用されます。
塑性#
材料は力の作用下で永久的な形状変化を生じ、破裂しない能力を持ちます。
断面収縮率#
$ \psi = \frac{A_0-A_1}{A_0}\times 100% $
ここで、A1 と A0 は試験片の破断部と元の断面積であり、単位は $ mm^2 $ です。
伸び率(延伸率)#
$ \delta = \frac{L_0-L_1}{L_0}\times 100% $
ここで、L1 と L0 は試験片の破断後と元のゲージ長さであり、単位は $ mm $ です。
韌性#
材料の破断時に必要なエネルギーを測定します。
衝撃韌性#
材料は衝撃荷重に対して破壊に抵抗する能力を持ちます。試験片が破断する際に消費される衝撃エネルギー $ A_k $(単位:$ J $):
$ A_k = mg\cdot h_1 - mg\cdot h_2$
衝撃韌性値 $ a_k $ は欠陥部位の単位断面積上の衝撃エネルギーであり、材料の衝撃韌性の大きさを表します。単位は $ J/cm^2 $ です:
$ a_k = \frac{A_k}{A_0} $
通常、塑性が良い材料ほど韌性も高くなります。
物質の強度、硬度、塑性、韌性の関係:
通常、材料の強度が高いほど、硬度も高くなります。
通常、材料の塑性が良いほど、韌性も良くなります。
通常、材料の強度と硬度が高くなると、塑性と韌性が低下します。
疲労強度#
疲労#
材料は交互荷重の作用下で、降伏強度以下で断裂する現象です。
疲労強度#
材料は規定回数の交互荷重の作用下で断裂せずに耐えられる最大応力であり、$ \sigma^{-1} $ で表され、疲労限界とも呼ばれます。
鋼材の $ \sigma^{-1} $ はおおよそその降伏強度 $ \sigma_b $ の半分であり、非金属材料の $ \sigma^{-1} $ は通常金属よりもはるかに低いです。
規定回数:
鋼材:$ 10^7 $
有色金属およびその合金:$ 10^8 $
この記事は Mix Space から同期更新され、xLog に掲載されています。
元のリンクは https://nishikori.tech/posts/tech/Mechanical-properties-of-materials です。